23+ Find eigenvalues online
If you find this content useful please consider supporting the work on Elsevier or Amazon. This formula is peculiar because it requires that we know St_j1 to compute St_j1However it happens that sometimes we can use this formula to approximate the solution to initial value problems.
Solved Algebra 2 Course Hero
Find eigenvalues given the characteristic polynomial without finding the.
. Where A is the matrix representation of T and u is the coordinate vector of v. Correlation and enrichment analyses of eigenvalues of the PC1 to various genomic and epigenomic features validated the similarity r 099 between our Control dataset and other Hi-C datasets. Compute the product of two matrices.
Eigenvalues and Eigenvectors in Python Though the methods we introduced so far look complicated the actually calculation of the eigenvalues and eigenvectors in Python is fairly easy. 123456 indicates 124 456i. The copyright of the book belongs to Elsevier.
The code is released under the MIT license. This always happens over mathbbC due to the Fundamental Theorem of Algebra but not always over mathbbR. The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillatorBecause an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point it is one of the most important model systems in quantum mechanicsFurthermore it is one of the few quantum-mechanical systems.
Here embedded eigenvalues occur at five k points over the first Brillouin zone. Lets look at some real life applications of the use of eigenvalues and eigenvectors in science engineering and computer science. R 023 P 0007.
Numerical data stored in comma separated value CSV. Before we give details on how to solve these problems using the Implicit Euler Formula we give another implicit formula called the Trapezoidal Formula which. Find the eigenvalues of a matrix.
The other four. 2060 1 1 gold badge 15 15 silver badges 23 23 bronze badges endgroup 6. It is not exactly true that non-square matrices can have eigenvalues.
They are used to reduce the dimension of large data sets by selecting only a few modes with significant eigenvalues and to find new variables that are uncorrelated. In the Standard Model of particle physics each different kind of elementary particle has four different charges corresponding to twists along directions of a four-dimensional maximal torus in the twelve. Mathematically these charges are eigenvalues of the Cartan subalgebra generators and are called roots or weights of a representation.
Given an x there is only one way to square it and then add 1 to the result. Matrix decompositions are a useful tool for reducing a matrix to their constituent parts in order to simplify a range of more complex operations. This first one is a function.
Googles extraordinary success as a search engine was due to their clever use of eigenvalues and eigenvectors. We find that its eigenvalues are either 1 textepm i theta for a rotation or pm 1 for a reflection. From the time it was introduced in.
Very helpful for least-square regressions. The eigenvector output you see here may not be the same as what you obtain on paper. We also have this interactive book online for a better learning experience.
This decomposition also plays a role in methods used in machine learning such. 243 Fast Fourier Transform FFT Contents 245 Summary and Problems. Apr 1 2017 at 2357 begingroup The first part seems accurate as long as the characteristic polynomial can be factored in linear terms as you did.
Indeed the definition of an eigenvalue is for square matrices. The main built-in function in Python to solve the eigenvalueeigenvector problem for a square array is the eig function in numpylinalg. And find their eigenvalues and eigenvectors in time proportional to a polynomial.
Complex numbers are stored in standard C notation which is a tuple surrounded by brackets. So no matter what value of x you put into the equation there is only one possible value of y when we evaluate the equation at that value of x. 686 published online 30 September.
These conclusions are supported by examining the eigenvalues both before and after principal axis extraction which yields a first factor explaining 31 of the variance in Study 1 and 35 of the variance in Study 2. Historically first and conceptually simplest is degree centrality which is defined as the number of links incident upon a node ie the number of ties that a node hasThe degree can be interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network such as a virus or some information. The bandwidth is minimized at θ m while being well separated from the.
The shooting methods are developed with the goal of transforming the ODE boundary value problems to an equivalent initial value problems then we can solve it using the methods we learned from the previous chapter. 1 1 2 99p 5 102 10 1000000 25 10 50 23 30 2 66. However this result appears to be largely mediated by social.
Why are eigenvalues and eigenvectors important. Solve sparse systems of linear equations. We have the following sequence of equalities since det A 1.
The learning machines we consider can be either classical 23242526272829303132 or quantum 89111333. In the initial value problems we can start at the initial value and march forward to get the solution. Here is a set of practice problems to accompany the Differentiation Formulas section of the Derivatives chapter of the notes for Paul Dawkins Calculus I course at Lamar University.
For non-square matrices we can define singular values. The bandwidth of the first band W and indirect band gap between the first two pairs of bands ε 12 and ε 23. But this method is not working for the.
The prefix eigen-is adopted from the German word eigen cognate with the English word own for proper characteristic own. Limited number of eigenvalues eigenvectors of sparse general square matrix. 4 begingroup Good short answer.
The convention used here is eigenvectors have been scaled so the final entry is 1. Perhaps the most used type of matrix decomposition is the eigendecomposition that decomposes a matrix into eigenvectors and eigenvalues. Eigenvalues and eigenvectors feature prominently in the analysis of linear transformations.
Without ads and with the simplest possible user interface. Originally used to study principal axes of the rotational motion. Our online number tools are actually powered by our programming tools that we created over the last couple of years.
In atomic physics the spin quantum number is a quantum number designated m s which describes the intrinsic angular momentum or spin angular momentum or simply spin of an electron or other particleThe phrase was originally used to describe the fourth of a set of quantum numbers the principal quantum number n the azimuthal quantum number l the. The one at Γ arises because symmetry forbids coupling to any outgoing wave 4. Remember you can have any scalar multiple of the eigenvector and it will still be an eigenvector.
The larger matrices involve a lot of calculation so expect the answer to take a bit longer.
Solved 1 1 Find A Full Singular Value Decomposition Svd Of The Matrix A 0 1 Course Hero

Browse Questions For Algebra
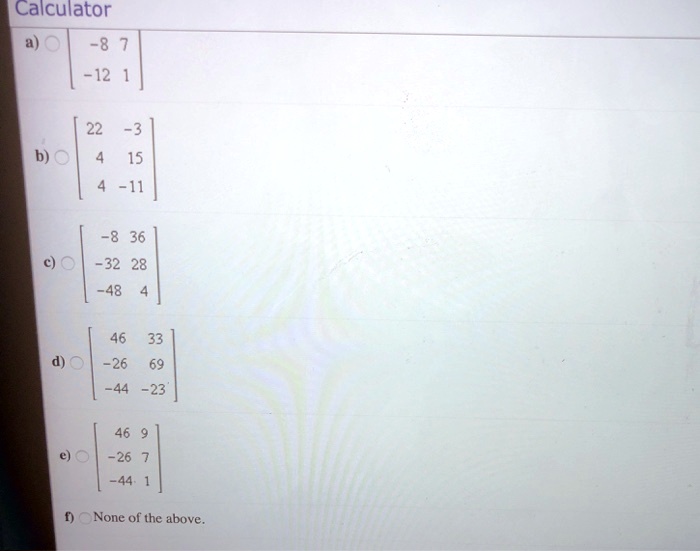
Browse Questions For Algebra
An Arithmetic Progression Has 41 Terms The Sum Of The First Five Terms Is 35 And Sum Of The Last Five Terms Is 395 What Is The First Term And The Common Difference Quora
Solved Algebra 2 Course Hero
What Is The Volume Of Solid Generated By Rotating An Ellipse Whose Equation Is Math Dfrac X 2 A 2 Dfrac Y 2 B 2 1 Math About Math Y Math Axis Quora
Solved 1 1 Find A Full Singular Value Decomposition Svd Of The Matrix A 0 1 Course Hero
Solved Subject Algebra 1 Topic Questions Answer Given Questions 1 20 Course Hero
How To Write This Log Equation As An Exponential Equation In 5 2x Quora
Solved Algebra 2 Course Hero
How To Find The X And Y Intercept Of Y 4 2x X 2 Quora

Example Find The Eigenvalues Eigenvectors Of A Matrix Basic Math Math Formulas Math Tricks
Solved Find An Invertible Matrix P And A Diagonal Matrix D Such That P 1 Ap D Course Hero
What Is The Second Derivative Of Y 2x 1 2 X 3 Quora
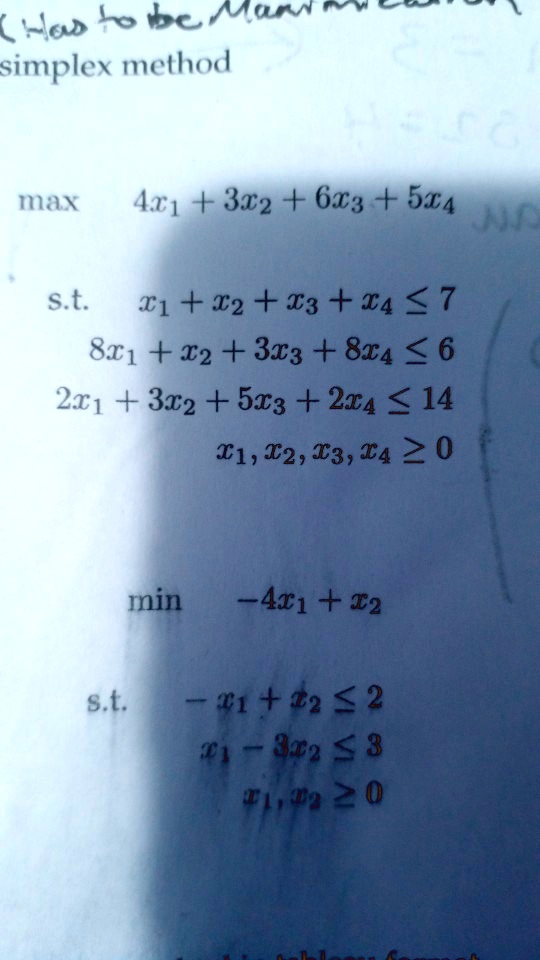
Browse Questions For Algebra
Solved Find An Invertible Matrix P And A Diagonal Matrix D Such That P 1 Ap D Course Hero
Solved 1 1 Find A Full Singular Value Decomposition Svd Of The Matrix A 0 1 Course Hero